¶ SPONGE增强抽样案例
更新时间:
2024/01/01
¶ 程序安装
¶ 什么是增强抽样?
通常,我们的分子动力学(MD)模拟在某一力场下进行,有势能函数
在该势能函数下,如果我们得不到需要的结果,此时可以使用增强抽样算法,在势能函数上添加上我们人为设定的偏置势(bias)
添加偏置势的模拟当然和真实模拟不同,但是可以根据计算进行转化,其理论基础是各系综下热力学量的分布函数计算,例如正则系综下有
这样我们模拟得到的结果每个出现的概率均做一个重加权即可,也即乘上
¶ 为什么使用增强抽样
这里,我们构建一个过氧化氢的模型体系,解压后的文件目录下为
│ H2O2_angle.txt
│ H2O2_bond.txt
│ H2O2_charge.txt
│ H2O2_coordinate.txt
│ H2O2_dihedral.txt
│ H2O2_exclude.txt
│ H2O2_LJ.txt
│ H2O2_mass.txt
│ H2O2_nb14.txt
│ H2O2_residue.txt
│
├─bad_normal_md
│ analysis.py
│ cv.txt
│ H2O2_dihedral.txt
│ mdin.txt
│
├─metadynamics
│ analysis.py
│ cv.txt
│ H2O2_dihedral.txt
│ mdin.txt
│
├─normal_md
│ analysis.py
│ cv.txt
│ mdin.txt
│
├─sits
│ analysis.py
│ cv.txt
│ H2O2_dihedral.txt
│ iteration.in
│ observation.in
│ production.in
│
└─umbrella_sampling
analysis.py
cv.txt
H2O2_dihedral.txt
min.in
run.in
run.py
这个模型体系中,我取消掉了过氧化氢的LJ和静电,只保留了键长、键角、二面角等内坐标的势能,让例子更简单以更方便了解原理和程序使用。
我们查看H2O2_dihedral.txt文件,有
2
2 0 1 3 2 0.3 0.4
2 0 1 3 3 0.1 -0.6
根据SPONGE文档中的文件格式和模块功能,我们可以知道这相当于势能函数
首先我们进入到压缩文件的normal_md文件夹中,在该文件夹中直接运行SPONGE。
SPONGE -mdin mdin.txt
在我们的mdin中,我们设置了我们的cv输入文件是cv.txt,其内容是
print
{
CV = torsion
}
torsion
{
CV_type = dihedral
atom = 2 0 1 3
}
我们在其中定义了一个名叫torsion,类型为dihedral,参数原子是2、0、1、3的CV
模拟结束过后,得到结果文件mdout.txt,我们使用以下python脚本(该目录下的analysis.py)进行分析
from Xponge.analysis import MdoutReader
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde
t = MdoutReader("mdout.txt")
t = t.torsion
kT = 8.314 * 300 / 4184
t = np.concatenate((t, t + np.pi * 2, t - np.pi * 2))
kernel = gaussian_kde(t, bw_method=0.03)
positions = np.linspace(-np.pi, np.pi, 300)
result = kernel(positions)
result = -kT * np.log(result)
result -= min(result)
theory = 0.3 * np.cos(2 * positions - 0.4) + 0.1 * np.cos(3 * positions + 0.6)
theory -= min(theory)
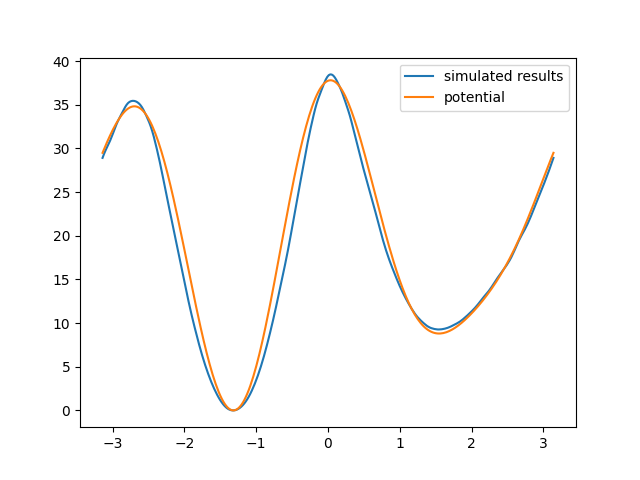
plt.plot(positions, result, label="simulated results")
plt.plot(positions, theory, label="potential")
plt.legend()
plt.show()
可见模拟得到的势能面与设定的二面角能量大致一致。虽然结果仍然不尽如人意,但是相信如果我们增加有限的模拟时长就能获得更好的采样结果。
那么我们现在进入bad_normal_md文件夹中,在这个文件夹中,我们的mdin中指定了替代默认dihedral的文件,在该文件中
2
2 0 1 3 2 15 0.4
2 0 1 3 3 5 -0.6
我们的势能函数直接乘了50,此时室温并不足以使得这个虚假的过氧化氢翻过二面角势垒
我们接下来也跑相同时间的MD模拟
SPONGE -mdin mdin.txt
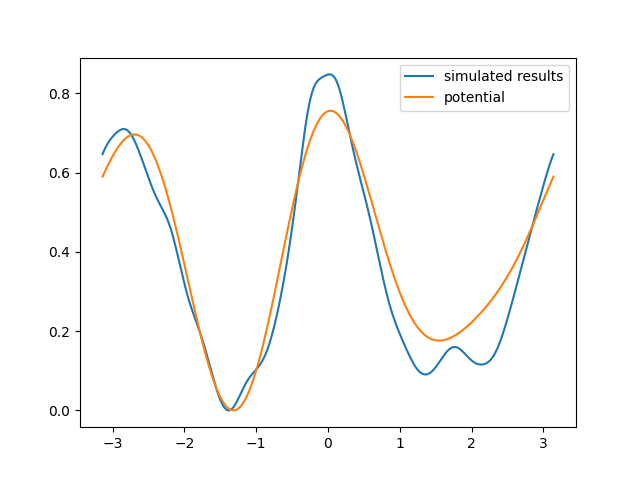
用上面相同脚本分析,得到结果如下:
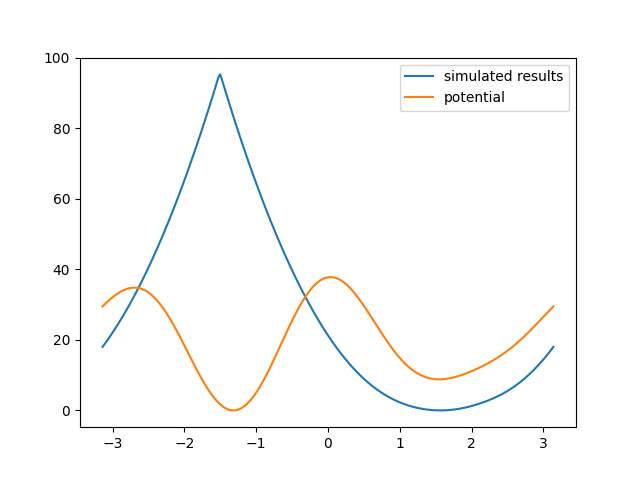
可见,此时模拟得到的结果已经非常不好,需要使用增强抽样算法。
¶ 伞形抽样
进入umbrella_sampling文件夹中,我们首先看看我们的cv.txt文件
print
{
CV = torsion
}
torsion
{
CV_type = dihedral
atom = 2 0 1 3
}
restrain
{
CV = torsion
weight = 200
reference = res_cv_ref
period = 6.283185308
}
这里,除了和普通md里一样的cv.txt以外,还加入了restrain部分,也就是简谐势限制。其中的参考值设为了res_cv_ref,由外部输入指定
编写python脚本run.py批量运行
import os
import shutil
import numpy as np
for i, ref in enumerate(np.linspace(-np.pi,np.pi,50)):
assert os.system(f"SPONGE -mdin min.in -res_cv_ref {ref}") == 0
assert os.system(f"SPONGE -mdin run.in -res_cv_ref {ref} -coordinate_in_file restart_coordinate.txt") == 0
shutil.copy("mdout.txt", f"{i}.mdout")
python run.py
最后获得了50份mdout
对于umbrella sampling,因为轨迹涉及很多个bias,需要使用WHAM算法重加权。我们使用下列脚本分析
import numpy as np
import matplotlib.pyplot as plt
from Xponge.analysis import wham
"""use help(wham.WHAM) to see the help"""
w = wham.WHAM(np.linspace(-np.pi, np.pi, 51), 300, 200, np.linspace(-np.pi, np.pi, 50), 2 * np.pi)
w.get_data_from_mdout("*.mdout", "torsion")
x, y, f = w.main()
plt.plot(x, y, label="umbrella sampling")
y2 = 15 * np.cos(2 * x - 0.4) + 5 * np.cos(3 * x + 0.6)
y2 -= min(y2)
plt.plot(x, y2, label="potential")
plt.legend()
plt.show()
最终得到的结果为
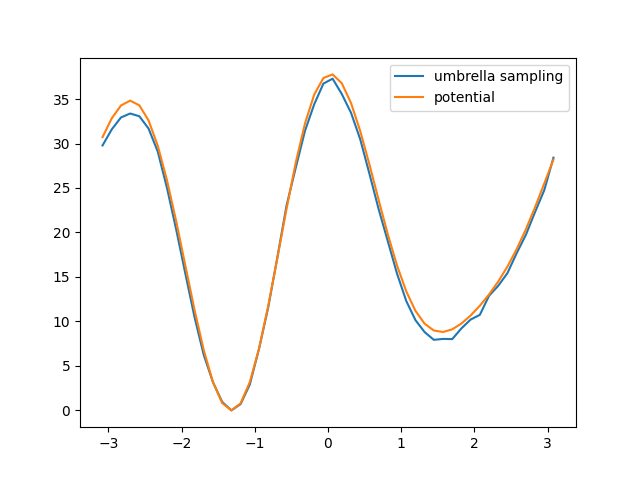

可见效果较好
¶ 埋拓动力学
进入umbrella_sampling文件夹中,我们首先看看我们的cv.txt文件
print
{
CV = torsion
}
torsion
{
CV_type = dihedral
atom = 2 0 1 3
}
meta1d
{
CV = torsion
dCV = 0.001
CV_minimal = -3.142
CV_maximum = 3.142
CV_period = 6.284
welltemp_factor = 50
height = 1
sigma = 0.5
}
这里,除了和普通md里一样的cv.txt以外,还加入了meta1d部分。具体含义可查询SPONGE文档
我们接下来也跑相同时间的MD模拟
SPONGE -mdin mdin.txt
使用下列脚本进行分析结果
from Xponge.analysis import MdoutReader
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde
t = MdoutReader("mdout.txt")
bias = t.meta1d
t = t.torsion
kT = 8.314 * 300 / 4184
w = np.exp(bias/kT)
t = np.concatenate((t, t + np.pi * 2, t - np.pi * 2))
w = np.concatenate((w, w, w))
kernel = gaussian_kde(t, weights=w, bw_method=0.01)
positions = np.linspace(-np.pi, np.pi, 300)
result = kernel(positions)
result = -kT * np.log(result)
result -= min(result)
theory = 15 * np.cos(2 * positions - 0.4) + 5 * np.cos(3 * positions + 0.6)
theory -= min(theory)
plt.plot(positions, result, label="simulated results")
plt.plot(positions, theory, label="potential")
toread = np.loadtxt("meta1d_potential.txt", skiprows=3)
toread[:, 1] = -toread[:, 1]
toread[:, 1] -= np.min(toread[:, 1])
plt.plot(toread[:, 0], toread[:, 1], label="meta1d potential")
plt.legend()
plt.show()
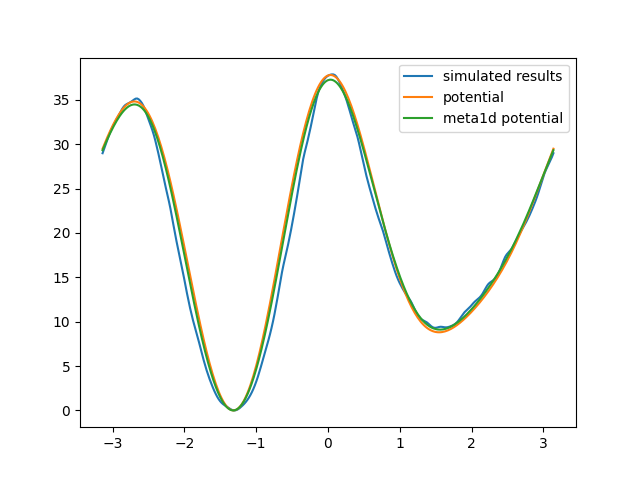
这里使用了两种得到结果的方式,一种是重加权,另外一种是直接使用metadynamics添加的势能函数的相反数,两种方式在此例中得到的效果相同。
使用metadynamics添加的势能函数的相反数得到自由能曲面时,因为使用了well-tempered metadynamics,所以实际上还要乘上一个因子,这个因子为
这里该因子
¶ 选择性温度积分增强抽样
注意,这里的例子本质是一个针对CV的抽样例子,并不太适合SITS,但原理是相同的
¶ 观察
首先,我们需要观察我们的体系。
SPONGE -mdin observation.in
在这个in文件里,我们加入了的额外命令是
SITS
{
mode = observation
atom_numbers = 4
}
sits_dihedral_in_file = H2O2_dihedral.txt
其中,SITS_mode = observation 表示观察,SITS_atom_numbers = 4表示我们对前4个原子的非键作用进行ITS,而sits_dihedral_in_file则指明我们希望进行ITS的二面角
运行时,我们主要观察其中的SITS_AA_kAB这一部分,这一部分是我们最终希望增强的能量。我们根据这个值的最小出现的值,减去一个预估的保留值,设置pe_b。
如此处,SITS_AA_kAB为9左右,我们预估后面会降低的值为20,设置的pe_b因此为-(9-20) = 11。
这里的pe_b选择是基于体系的。你需要合理调节pe_b的值,否则系统很有可能出现崩溃!
接下来,我们就进行迭代处理
SPONGE -mdin iteration.in
在这个in文件里,我们加入了的额外命令是
SITS
{
mode = iteration
atom_numbers = 4
T_high = 8000
k_numbers = 8000
T_low = 200
pe_b = 11
}
sits_dihedral_in_file = H2O2_dihedral.txt
这个部分新增包括积分的最高温度、积分的最低温度和积分的离散格点数,以及上面提到的pe_b。这些参数都是可以调节的,而较差的参数可能会引起势能函数突变,进而模拟崩溃。
该步模拟后,最重要的就是获得SITS_nk_rest.txt文件,该文件包含了不同温度的自由能信息,我们用该文件进行生产模拟
SPONGE -mdin production.in
在这个in文件里,我们加入了的额外命令是
SITS
{
mode = production
atom_numbers = 4
T_high = 8000
k_numbers = 8000
T_low = 200
pe_b = 11
nk_in_file = SITS_nk_rest.txt
}
sits_dihedral_in_file = H2O2_dihedral.txt
这部分新增加的就是iteration部分获得的SITS_nk_rest.txt作为输入,给到nk_in_file命令。
模拟结束后使用下列脚本进行分析
from Xponge.analysis import MdoutReader
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde
t = MdoutReader("mdout.txt")
bias = t.SITS_bias
t = t.torsion
kT = 8.314 * 300 / 4184
w = np.exp(bias/kT)
t = np.concatenate((t, t + np.pi * 2, t - np.pi * 2))
w = np.concatenate((w, w, w))
kernel = gaussian_kde(t, weights=w, bw_method=0.01)
positions = np.linspace(-np.pi, np.pi, 300)
result = kernel(positions)
result = -kT * np.log(result)
result -= min(result)
theory = 15 * np.cos(2 * positions - 0.4) + 5 * np.cos(3 * positions + 0.6)
theory -= min(theory)
plt.plot(positions, result, label="simulated results")
plt.plot(positions, theory, label="potential")
plt.legend()
plt.show()
得到结果如下: